TX_four_square

Four-Square

The 220-ft tower has five catenary lines, each about 500 feet long. Four of these lines, running NE, SE, SW, and NW support four 1/4-wavelength wire verticals used in a 160-meter four-square antenna. 

Each four-square element is made from a single # 9 AWG aluminum wire. The elements are fed with 50-ohm foam dielectric coaxial cables. Each element has about fifty 1/4-wavelength radials. These radials are bonded to the large radial system of the 200-foot tower at points where more than two wires cross. This makes the entire grounding system for the 200-foot and four-square elements more similar to a large screen rather than just than individual radials.

Four-Square Design

One item overlooked throughout the history of the four-square is the effective element spacing. Effective element spacing is not the same as the distance along each side of the square. The effective spacing is less than that distance, because the array fires from corner to corner. The effective array length is 1.414 times the spacing along each side, not twice that length. With 90 degree per side array size, we really only have a 127 degree long end-fire array when firing across diagonal corners. The correct phasing for an optimum null at zero degrees elevation directly in line with the array is not 90 and 180 degrees, but is actually around 117 and 234 degrees! With the traditional 90 and 180 degree phasing, the array should be stretched to a corner-to-corner distance of 180 degrees, making each side 127 degrees long. Unfortunately feedlines of 1/4-wl electrical length won't reach that distance with velocity factor and connection lengths involved, so the obvious choice is to use greater than 90-degree phase shift. As an additional benefit, the directivity and gain are higher with closer spacing and larger phase shift. Performance is better for both receiving and transmitting.             

The phase and spacing used are obviously not optimum, and the popular coupling units almost certainly do not do what we expect. They sacrifice gain because any four-square 1/4 wl on a side really does not "want" 90- and 180-degree phase shift, and they really are not designed for the real impedance presented by the feedlines from the elements. Why do we use such a design? Probably because it was originally used, and no one ever looked at the array in any detail. It was easy to copy the original concepts, and no one thought to check and see if the phasing systems were optimized.   

Array Transmission Lines

(the following assumes lines have negligible loss)

I use 1/4-wavelength 50-ohm lines feeding each four-square element. 1/4-wavelength lines have a unique property. When odd-quarter-wave lines are sourced from equal voltages, the load ends of the line will source equal currents into any load impedance.

There is a second important often overlooked property of transmission lines used in phase-critical systems. When a transmission line is misterminated, the line has standing waves. When there are standing waves, phase shift of the line no longer equals the electrical length of the line. An exception occurs when the line is any multiple of 90-degrees.  

Just as impedances invert every 1/4 wl, the fixed source voltage at one end becomes a fixed source current at the other end. Not only that, phase shift is constant even though the lines are terminated by different load impedances. Many arrays use this concept to advantage.

By the way, a current sourced 1/2 wl line would work just as well as the 1/4 wl lines if we fed the line with equal currents instead of equal voltages. (As a matter of fact that concept is behind a two-band transmitting array I designed.) 

Current Distribution

A two-element directional system requires equal current at the current maximum of each directional element for maximum F/B ratio and gain. A three-element array would require a binomial 1:2:1 ratio for best pattern. The center element, in effect, has to supply a field for each of the two outer elements to work against, it is doing double duty. The four-square is a novel approach to a three-element array, the center two elements are fed in phase, and act as one common element. If all four elements have equal current, total center element current is twice the current in each end. The 1:2:1 current distribution is satisfied.

With elements series-fed at the point of current maximums, each element requires equal current at the feedpoint. (If the elements were voltage-fed at the voltage maximum, they would require equal voltages at the feedpoint to have equal currents in the elements!) This makes transmission-line type phasing systems easy to design. We simply design the system so each phasing-line has unity standing wave ratio, and tie the elements directly to the phasing lines. Because voltages are equal everywhere in the phasing system, element currents are equal at the end of each 1/4-wavelength feedline.

Phasing Systems

My design operates the phasing line without standing waves. Since the phasing line is not a multiple of 1/4-wl, if the delay line were misterminated phase shift would not equal the line electrical length. Voltage at each end of the delay line would also be different. Since the line is matched, phase shift will be equal to the electrical length of the line and voltages will be equal at each end of the delay line.

There really isn't any need for "dump" resistances or hybrids in any phasing system. If you look at the systems, the dump resistances really don't guarantee performance. A four-square system never requires controlled "power splitting". As a matter of fact, equal power in each element would guarantee poor F/B ratio and gain. The only way to obtain satisfactory F/B ratio with a hybrid coupler is to somehow mess up the hybrid so it doesn't act like a real hybrid!!

Keep in mind that each element, other than the two in parallel, has a different feed impedance. With different load impedance at each element current can't be equal in each feedline element group if power is divided evenly. The four-square system, at least one with 1/4 wl feedlines, actually requires equal voltages. Equal power insures a poor pattern, while equal current at the element (or equal voltage at the start of the 1/4 wl feedlines) guarantees optimum patterns. Most four-squares work as well as they do only because the array is somewhat forgiving. They are a good example of reasonable performance through oversight, rather than careful planning.

I solved these problems in my system by placing the phasing common-point in the direction of maximum radiation and using crossfire phasing. This is very similar to the feed-system of a log periodic, except I optimized phase shift and current distribution.

A crossfire delay line system feeds the center two elements in my array. This is similar to the scheme I use in my phased receiving antennas. Each center element has around 25 ohms of operating impedance, and that produces 100 ohms at the end of the 1/4-wavelength 50-ohm feedline that goes to each element. The center two elements, when paralleled, have a combined impedance of 50 ohms.

The delay line from the common point to the center two element junction is 60-degrees of RG-8 coax. The 180-degree "flip" comes by using a choke balun. This is similar to the technique I use in receiving antennas.  The primary difference is in core size and materials, my high-power inverting transformer uses eight 2-inch diameter 65-material cores and Teflon insulated coaxial cable. This choke allows the shield and center to be transposed at one end of that delay line. Loss is low in the delay system, because it is a matched 50-ohm line. It is also only 60-degrees long and only handles only about 2/3 of total system power (almost 1/3 of the system power is applied directly to the front element).    

The rear element offers a slight problem, because that element has a very low impedance. It almost has enough current, through mutual coupling alone, to be fully functional. As a consequence, it requires very little common point power. With a 1/4-wavelength feedline and parallel reactance canceling, the rear element presents several hundred ohms of resistance to the phasing network. My solution for feeding the rear element was to build an artificial transmission line using lumped components. For the rear delay line, I used multiple L/C sections to simulate a transmission line with a characteristic impedance matching the rear element. This has three advantages:

1.) Q is low, making phase-shift much less frequency critical.

2.) Voltage is equal at each end of the artificial transmission line, allowing the delay line to all parallel each other at the common point.

3.) I can easily "tweak" delay line characteristics with a few adjustments and optimize the array null.

In effect, I created a high-impedance transmission line from individual L/C components, and only needed to use 120 degrees of lag (the 240 degree lead I needed is electrically the same as a 120 degree lag) in the network. This is all very similar to the system in my small receiving four-square. Because current is low, components can be modest sized. The end result is more bandwidth, more stability, and less loss than a simple one-stage network.

The Results

While this may sound like a complex system, it is very simple in practice. This array has exceptional bandwidth, exhibiting useful F/B ratio and gain over the entire 160-meter band. This also means a similar array for 80-meters would cover almost all of 80 and 75 meters. Additionally, this array has very low loss regardless of operating frequency. It does not divert power into a dump resistance.

My phasing design produces higher gain than conventional 90/180 degree phased four-squares through a tighter pattern and less loss.

Because the pattern is "tight", I added a simple system that provides a wide East, South, West, or North pattern. That pattern nearly equals the gain from a traditional four-square, and provides equal or better gain than traditional four-squares in all directions over a wider frequency range.

Here is the pattern of a traditional four-square at 15 degrees elevation, assuming perfect distribution and phase. This neglects losses in the Hybrid dump resistor, and phase and current distribution errors:

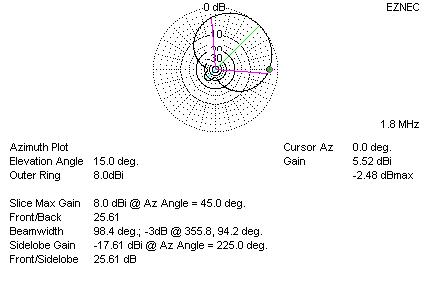
Note the gain is 8dBi, and the 90-degree azimuth gain is -2.5dB maximum or a net gain of 5.5dBi in the "between" directions  

Here is the pattern of the same array with 120/240 degree phasing:

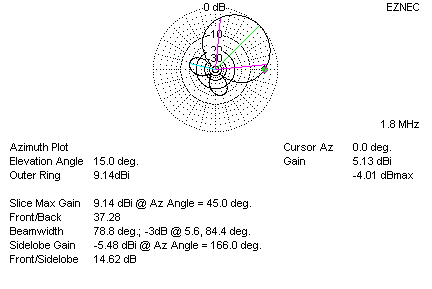
The gain is 9.14dBi, and the cursor azimuth gain is -4 dB maximum for an "in between" gain of 5.13dB. You only give up .4dB FS at the worse point for a net gain of 1.14dB in primary directions.

Gain increase over an optimized Hybrid coupler system is just over 1 dB from the increased directivity. In addition to that, there is also decreased loss. F/B ratio change is quite noticeable, as is the ability of the antenna to receive.

My actual working array is even more flexible, allowing the choice of eight directions plus omni. 

In concert with a large ground system (the array sits in an area that has ground systems extending for at least a half-wavelength in all directions) and reduced loss in the phasing system, overall performance has been enough to offset salt-water path and distance advantages of northeast stations using smaller Hybrid Coupler systems.